###############################################################################
# Analisis de redes sociales y capital social (2017)
###############################################################################
library(sna)
###############################################################################
# Simulamos una matriz y creamos variables o atributos de los actores
# Creamos un vector con los nombres de los actores
nombres<- c( "Jose",
"Romina","Alicia","Maco","Jesica",
"Armando",
"Fabiola","Tatiana",
"Julio","Pedro", "Juan", "Kike", "Rolas", "Roberto")
# Como primer atributo de los actores creamos un vector con el género
sexo= c("M",
"F","F","F","F",
"M",
"F","F",
"M","M","M","M","M","M" )
# El año en que concluyeron sus estudios de licenciatura
graduados=c(sample(1990:2012,
length(nombres),
replace = TRUE))
# Desde el punto de vista social: liberal o conservador
# Liberal= pro-eleccion (aborto), matrimonios del mismo sexo...
perspectiva_social= c(sample(c("L", "C"),
length(nombres),
replace = TRUE))
###############################################################################
# FUNCION 1
###############################################################################
# Comparo el sexo el elemento 1 del vector, o sea de José con el del resto de los
# actores, si es igual da TRUE sino FALSE
# atributo 1 vector variable categórica, homofilia (0-1), etiquetas
# vector con el nombre o etiqueta de los actores
comparar_attributos <- function(atributo1,etiquetas,homofilia){
xeAll=vector()
for(i in 1:length(atributo1))
{xen=atributo1[i]==atributo1 #comparo cada actor con el resto
xeAll=c(xeAll,xen)
}
A = matrix(
xeAll, # elementos
nrow=length(atributo1), # hileras
ncol=length(atributo1), # columnas
byrow = TRUE) # llenar por hileras
#################################################################################
# asigno lazos en base a homofilia
for(i in 1:nrow(A))
{
for(j in 1:ncol(A))
{ ###########checa solo cambie las reglas
if (A[i,j]) {A[i,j]=rbinom(1,1,homofilia)} else # homofilia
{A[i,j]=rbinom(1,1,1-homofilia)}
}####cierro loop para row (hileras)
}####cierro loop para col (columnas)
#################################################################################
#### nombres
colnames(A)<-etiquetas
rownames(A)<-etiquetas
#diagonal la vuelvo ceros
diag(A)<-0
A
} #### cierro la función
##################################################################################
#### USAMOS LA FUNCION 1
#### para crear una variable dependiente
#### usamos una vinculación preferencial del 50% o más bien no hay preferencia
#### para vincularse dado el género de los actores
colaboracion=comparar_attributos(sexo,nombres,0.50)
colaboracion; class(colaboracion); dim(colaboracion)
###############################################################################
# Algunas ocasiones hay problemas con los acentos
# Acentos
# \u{ED} i con acento
# \u{E1} a con acento
# \u{F3} o con acento
# \u{F1} ñ
# \u{E9} e con acento
# \u{FA} u con acento
###############################################################################
#### visualizamos la gráfica
### FIGURA 1
###############################################################################
plot.sociomatrix(colaboracion, asp=0.5,
main="Figura 1. red de colaboraci\u{F3}n, preferencia por el mismo g\u{E9}nero 50%")
###############################################################################
# FUNCION 2
###############################################################################
### Esta función crea una matriz que adopta valores de 1 si el actor i y el
### actor j comparten el mismo atributo
comparar_binario <- function(atributo2,etiquetas){
xeAll=vector()
for(i in 1:length(atributo2))
{xen=atributo2[i]==atributo2 #comparo cada actor con el resto
xeAll=c(xeAll,xen)
}
A = matrix(
xeAll, # elementos
nrow=length(atributo2), # hileras
ncol=length(atributo2), # columnas
byrow = TRUE) # llenar por hileras
##############################################################################
# asigno lazos en base a homofilia
for(i in 1:nrow(A))
{
for(j in 1:ncol(A))
{ ###########checa solo cambie las reglas
if (A[i,j]) {A[i,j]=1} else # 1 si ambos comparten un atributo
{A[i,j]=0}
}####cierro loop para row (hileras)
}####cierro loop para col (columnas)
#############################################################################
#### nombres
colnames(A)<-etiquetas
rownames(A)<-etiquetas
#diagonal la vuelvo ceros
diag(A)<-0
A
} #### cierro la función
###############################################################################
### Usamos la FUNCION 2 para crear una variable independiente
A_sexo=comparar_binario(sexo,nombres)
###############################################################################
# Coeficiente de correlacion
diag(colaboracion)<-NA
diag(A_sexo)<-NA
cor(as.vector(colaboracion), as.vector(A_sexo), use = "complete.obs")
###############################################################################
colab_qap=qaptest(list(colaboracion,A_sexo), gcor, g1=1, g2=2, reps=10000)
summary(colab_qap)
colab_qap$pgreq
colab_qap$pleeq
colab_qap$testval
colab_qap$dist
###############################################################################
# Figura 2
###############################################################################
d <- density(colab_qap$dist)
plot(d,lwd=2, main="Figura 2. QAP: 10 mil replicas del coeficiente de correlaci\u{F3}n",
xlab="Coeficiente de correlaci\u{F3}n", ylab="Densidad")
polygon(d, col="grey", border="black");abline(v=colab_qap$testval,col="red", lwd=2, lty=3)
polygon(c(d$x[d$x>=colab_qap$testval], colab_qap$testval ), c(d$y[d$x>=colab_qap$testval],0 ), col="red")
legendXY<-locator(1)
text(legendXY, paste("Área coeficiente > \n",round(colab_qap$testval,3), "=",colab_qap$pgreq), cex=.85, col="white")
###############################################################################
# ¿existe una preferencia a colaborar con actores sociales del mismo género?
# Homofilia de género.
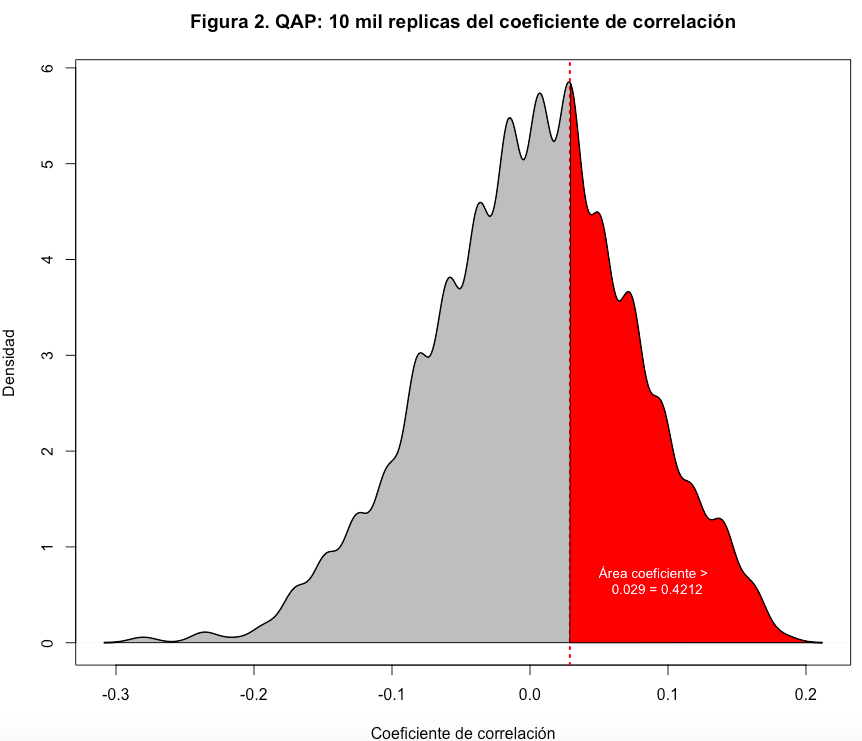
# No se observó una vinculación preferencial de género en la red de colaboración,
# tal como lo indica el coeficiente de correlación r = 0.02886951 (p = 0.4212).
###############################################################################
# FUNCION 3
###############################################################################
### Esta función se utiliza también para construir una matriz de variables
### independientes. En este caso calcula la diferencia absoluta del valor
### de la variable "x" entre los actor i y j
comparar_dif_abs <- function(atributo3,etiquetas){
xeAll=vector()
for(i in 1:length(atributo3))
{xen=abs(atributo3[i]-atributo3) #comparo cada actor con el resto
xeAll=c(xeAll,xen)
}
A = matrix(
xeAll, # elementos
nrow=length(atributo3), # hileras
ncol=length(atributo3), # columnas
byrow = TRUE) # llenar por hileras
#### nombres
colnames(A)<-etiquetas
rownames(A)<-etiquetas
#diagonal la vuelvo ceros
diag(A)<-NA
A
} #### cierro la función
##################################################################################
# Aplicamos la FUNCION 3
A_grad=comparar_dif_abs(graduados,nombres)
##################################################################################
grad_qap=qaptest(list(colaboracion,A_grad), gcor, g1=1, g2=2, reps=10000)
summary(grad_qap)
plot(grad_qap, xlim=c(-0.7, 0.4))
### en este caso tampoco hay correlaciion ni es esta significativa
###############################################################################
# FUNCION 4
###############################################################################
# Esta funcion se puede modificar de muchas formas, la idea es de que
# a mayor diferencia absoluta entre el valor de una variable para dos
# actores menos probabilidad de ocurrencia de un lazo
# beta1 adopta entonces un valor negativo (0.1 a 0.5)
# se recomienda al lector personalizar la sensibilidad de estos valores
comparar_attributos1 <- function(atributo4,etiquetas,beta1){
x1=as.vector(atributo4) # vectorizo
beta0 <- mean(x1, na.rm=T) # el promedio
beta1 <- beta1 # sensibilidad
pi_x <- exp(beta0 + beta1 * x1) / (1 + exp(beta0 + beta1 * x1))
y <- rbinom(n=length(x1), size=1, prob=pi_x)
A = matrix(
y, # elementos
nrow=length(etiquetas), # hileras
ncol=length(etiquetas), # columnas
byrow = TRUE) # llenar por hileras
#### nombres
colnames(A)<-etiquetas
rownames(A)<-etiquetas
#diagonal la vuelvo ceros
diag(A)<-NA
A
}
###############################################################################
Colaboracion_grad=comparar_attributos1(A_grad,nombres, -0.3)
cor(as.vector(Colaboracion_grad), as.vector(A_grad), method = "pearson", use = "complete.obs")
grad_qap=qaptest(list(Colaboracion_grad,A_grad), gcor, g1=1, g2=2, reps=10000)
summary(grad_qap)
grad_qap$pgreq
grad_qap$pleeq
grad_qap$testval
grad_qap$dist
###############################################################################
# Figura 3
###############################################################################
d <- density(grad_qap$dist)
plot(d,lwd=2, main="Figura 3. QAP: 10 mil replicas del coeficiente de correlaci\u{F3}n",
xlab="Coeficiente de correlaci\u{F3}n", ylab="Densidad", xlim=c(-0.4, 0.3))
polygon(d, col="grey", border="black");abline(v=grad_qap$testval,col="red", lwd=2, lty=3)
polygon(c(d$x[d$x>=grad_qap$testval], grad_qap$testval ), c(d$y[d$x>=grad_qap$testval],0 ), col="red")
legendXY<-locator(1)
text(legendXY, paste("Área coeficiente < \n",round(grad_qap$testval,3), "=",grad_qap$pleeq), cex=.85, col="black")
###############################################################################
QAP Correlación entre matrices
Dr. Luis Alan Navarro Navarro
Centro de Estudios en Gobierno y Asuntos Públicos
El Colegio de Sonora
QAP son las siglas en Inglés para "Quadratic Assignment Procedure", se traduce al Español como: "paradigma de asignación cuadrática" o "procedimiento de asignación cuadrática". Usamos QAP ya que nos interesa probar la significancia estadística de una correlación, específicamente, el coeficiente de correlación de Pearson. En el análisis de redes sociales se busca conocer si la existencia de un tipo de relación entre dos actores sociales (personas, organizaciones, etc.) esta correlacionada con la presencia de un vínculo o lazo de interés.
Una de las características fascinantes del QAP es que hace explicita la forma en la que probamos la "significancia estadística", un término común en el lenguaje de científicos que basan sus investigaciones en métodos cuantitativos. La "significancia estadística" se sustenta en la rareza de un hallazgo (traducido como un indicador o parámetro), dentro de un conjunto de datos que son una muestra del aleatoria de dicho indicador o parámetro. Esta muestra aleatoria se conoce como la distribución de la hipótesis nula, son los valores que asumiría el indicador si consideramos no rechazar la hipótesis nula. Por ejemplo: hipótesis nula (Ho): el género (sexo) de los actores sociales no influye su preferencia a asociarse o colaborar, la hipótesis alternativa es lo contrario, que si existe una propensión a asociarse con personas del mismo sexo.

La figura 1 muestra una sociomatriz con datos simulados. Es una matriz cuadrada no simétrica, dónde las celdas en color negro representan la existencia de un lazo de colaboración entre los actores. La probabilidad de elegir entre un colaborador hombre o mujer es del 50%, por lo que podemos asumir que el género no influye las preferencias a asociarse entre el grupo de actores que se estudia. Esperamos que el coeficiente de correlación entre la matriz de colaboración (figura 1) y la matriz de similitud de género (una matriz cuyas entradas asuman un valor de 1 si el sexo del actor "i" es igual al del actor "j", y 0 de otra forma), sea muy bajo y estadisticamente no significativo.
El coeficiente de correlación es de 0.03, muy bajo. Lo que hace QAP es crear una distribución nula, esta distribución se crea permutando una de las matrices (por ejemplo la de "similitud de género") y calculando de nuevo el coeficiente de correlación, esto se repite 10,000 veces (ver figura 2).
Ahora supongamos que observamos la variable año de obtención (graduación) del título profesional. Se espera que aquellos con menor diferencia absoluta para esta variable, sean más similares en su forma de pensar, perspectiva profesional y seguramente con menor diferencia de edad. Por lo tanto, esperaríamos un coeficiente de correlación negativo, esto es, a menor diferencia mayor probabilidad de que exista un lazo de colaboración entre los actores.
Se simula una matriz de colaboración basada en la matriz de diferencias absolutas. Se obtiene un coeficiente de correlación de -0.20 y estadísticamente significativo (P < 0.05) (ver figura 3).
Al momento de estimar el coeficiente de correlación, se debe de tomar en cuenta la magnitud de éste y como es el caso, la significancia estadística. Estimada aquí con una técnica no paramétrica. Abajo se anexa el código de R, considerando que posee muchas funciones que generan valores al azar, el lector obtendrá valores diferentes a los que aquí se presentan. Sin embargo, el presente tutorial puede modificarse y generalizarse a diferentes bases de datos.